
[高校数学]ベクトルの解法
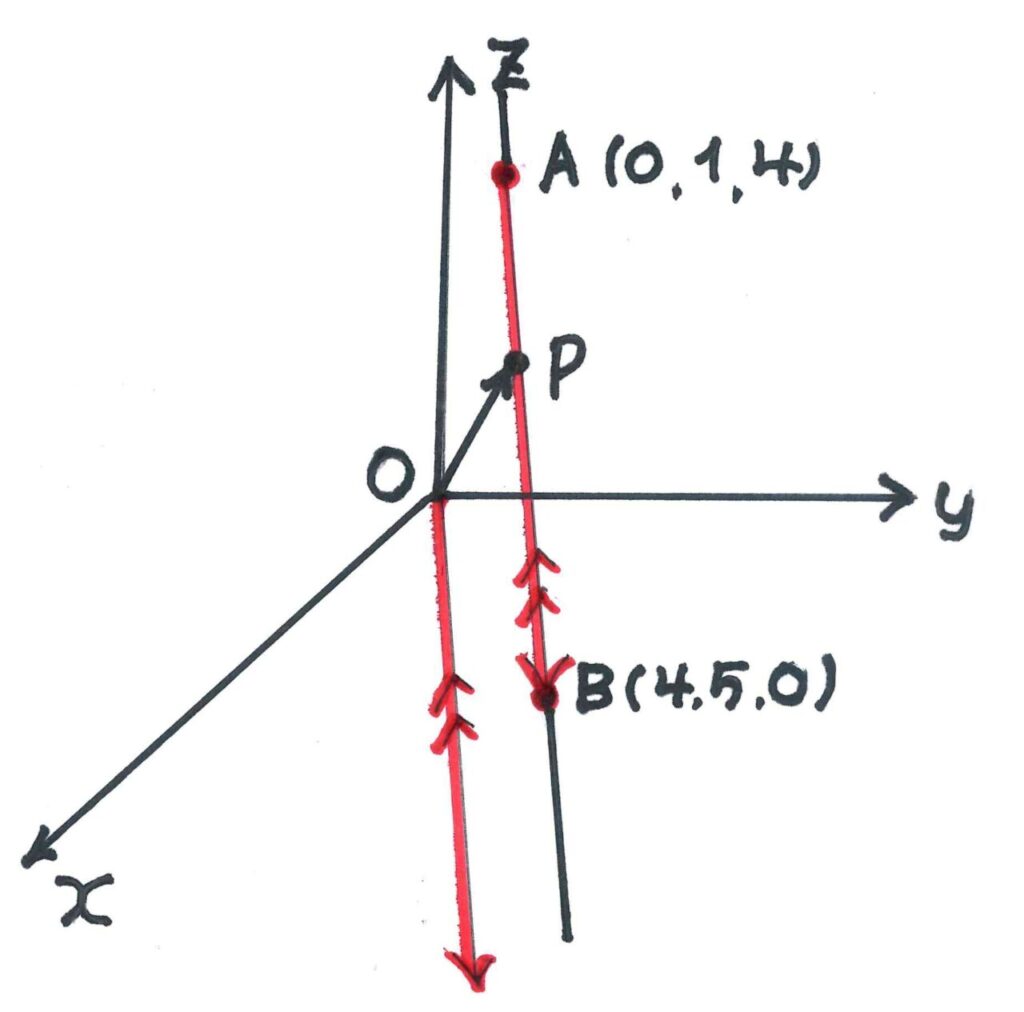
2点 A(0,1,4),B(4,5,0)を通る直線l上の点Pにおいて,
原点Oと点Pを結ぶ直線mと直線 l が直交するとき点Pの座標を求めよ
という教科書にある問題について考えます。
まず直線mを点Pのベクトル方程式としてパラメータtを使い表せば、
OP(m)=OA+tAB=(4t, 1+4t, 4-4t)(成分表示)。
直線 l と平行なABを原点を始点とした位置ベクトルとみれば(4, 4, -4)と表せます。
また直交とは垂直に交わることであり、垂直とは違います(垂直は平行移動してもなす角が90°であればOKです)。
ここでは向きと大きさを持つベクトルの話(場所は問わないってこと)なので、平行移動したうえで交わればいいわけで事実上垂直と同じ意味になります。
さて、直線mが(4t, 1+4t, 4-4t)で直線lと平行なABが(4, 4, -4)と表せましたが、ここの問題ではこれらが直交するとありますのでベクトルの問題では内積=0が使えそうです。
(イメージとしてはベクトルの始点をOとしたABがOP(m)と直交する感じです)
(4t ,1+4t, 4-4t)・(4, 4, -4)=48t-12=0→t=1/4。
よって、OP(→)=(1,2,3)となり、原点を始点とする位置ベクトルですから点Pは(1,2,3)となります。
葛飾区の学校を知りつくした定期テスト対策
エマールゼミは55年以上に渡って葛飾区の中学生や高校生を指導してきたお花茶屋の地域塾です。その指導の中で蓄積されたノウハウやデータをもとに定期テスト対策をおこないます。

